原始题目：剑指 Offer 66. 构建乘积数组 (opens new window)

解题思路：

这道题的难点除了不能使用除法外，还不能使用暴力法去解，会超时。因此最好还是能在计算 $B[i]$ 时，能复用 $B[i-1]$ 的计算结果。

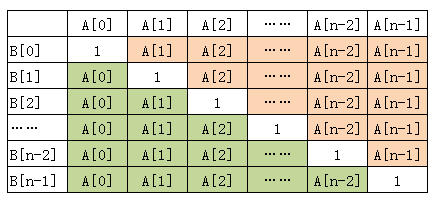
$B[i]$ 的定义如上图所示，将表格分为上三角和下三角，分别计算两个三角形的，就可以得到 $B[i]$ 的乘积。

算法流程：

1. 初始化：数组 $B$，其中 $B[0] = 1$；
2. 计算 $B[i]$ 的下三角各元素的乘积，$i$ 从 $0$ 到 $n -1$ 递增。计算 $B[i]$ 时，要借助 $B[i-1]$ 减少运算次数，$B[i] = B[i-1] \times A[i-1]$；
3. 计算 B[i] 的上三角各元素的乘积，$i$ 从 $n-2$ 到 $0$ 递减。使用辅助变量 $tmp$，用来存储计算过的结果（好像第 $2$ 步里的 $B[i-1]$ 的作用）。
4. 返回 B。

代码：

public int[] constructArr(int[] a) {
    if (a == null || a.length == 0) {
        return new int[0];
    }
    int[] ans = new int[a.length];
    ans[0] = 1;
    for (int i = 1; i < ans.length; i++) {
        ans[i] = ans[i - 1] * a[i - 1];
    }
    int tmp = 1;
    for (int i = ans.length - 1; i >= 0; i--) {
        ans[i] *= tmp;
        tmp *= a[i];
    }
    return ans;
}

复杂度分析

• 时间复杂度$O(N)$：其中 $N$ 为数组的长度，两轮遍历，使用 $O(N)$ 时间。
• 空间复杂度$O(1)$：辅助变量占用 $O(1)$ 的复杂度。